- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄353141 > GM123210NFEAB-01 (Electronic Theatre Controls, Inc.) LCD MODULE SPECIFICATION PDF資料下載
參數(shù)資料
| 型號(hào): | GM123210NFEAB-01 |
| 廠商: | Electronic Theatre Controls, Inc. |
| 英文描述: | LCD MODULE SPECIFICATION |
| 中文描述: | 液晶模組規(guī)格 |
| 文件頁數(shù): | 16/20頁 |
| 文件大?。?/td> | 218K |
| 代理商: | GM123210NFEAB-01 |
Confidential Document
Page:
5 /20
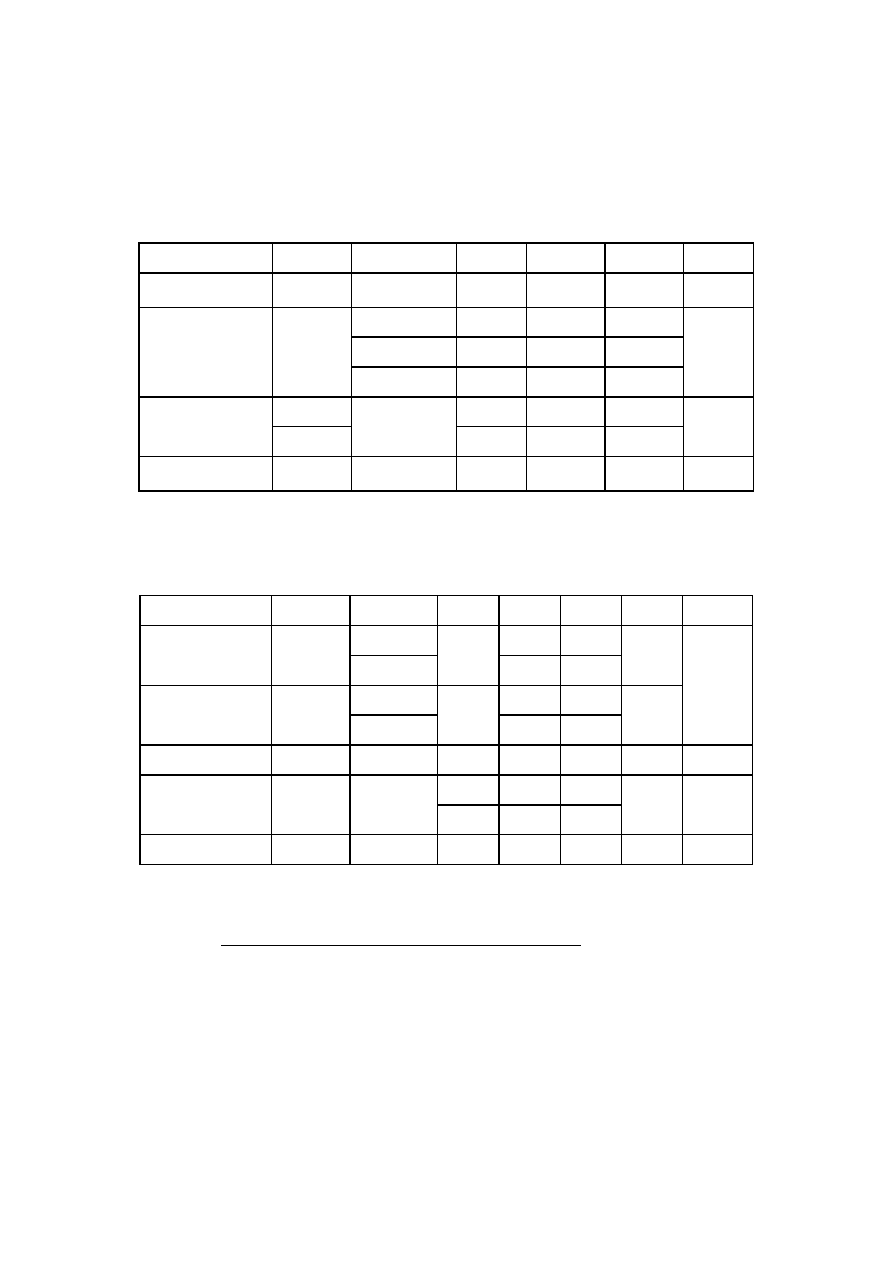
5. ELECTRICAL CHARACTERISTICS
Item
Symbol
Condition
Min.
Typ.
Max.
Unit
Supply Voltage
(Logic)
VDD-VSS
2.7
5.0
5.5
V
-20
°C
6.9
7.5
8.1
25
°C
5.8
6.4
6.9
Supply Voltage
(LCD)
VDD-VEE
70
°C
4.8
5.3
5.8
V
VIH
VSS+2.0
--
VDD
Input Voltage
VIL
--
VSS
--
VSS+0.8
V
Logic Supply
Current
IDD
VDD-VSS=5V
--
1.2
--
mA
6. ELECTRO-OPTICAL CHARACTERISTICS
ITEM
Symbol
Condition
Min.
Typ.
Max.
Unit
Ref.
0
°C
--
Rise Time
Tr
25
°C
--
120
240
ms
0
°C
--
Fall Time
Tf
25
°C
--
200
350
ms
Note (1)
Contrast
CR
25
°C
3
4
--
Note (3)
--
80
View Angle
θ1~θ2
1, 2
25
°C &
CR
≥1.5
-30
--
30
Note (2)
Frame Frequency
Ff
25
°C
--
64
--
Hz
Note (1) & (2) : See next page
Note (3) : Contrast ratio is defined under the following condition:
CR=
Brightness of non-selected condition
Brightness of selected condition
( a ).
Temperature ---------- 25
°C
( b ).
Frame frequency ---- 64Hz
( c ).
Viewing angle --------
θ= 0°, = 0°
( d ).
Operating voltage --- 6.4V
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| GM123210GFSAB-01 | LCD MODULE SPECIFICATION |
| GM123210GFSBB-01 | LCD MODULE SPECIFICATION |
| GM123210GRSAB-01 | LCD MODULE SPECIFICATION |
| GM123210GRSBB-01 | LCD MODULE SPECIFICATION |
| GS71024T-9I | 64K x 24 1.5Mb Asynchronous SRAM |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| GM123210NFEBB-01 | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:LCD MODULE SPECIFICATION |
| GM123210NFENB-01 | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:LCD MODULE SPECIFICATION |
| GM123210NFEWB-01 | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:LCD MODULE SPECIFICATION |
| GM123210NFEYB-01 | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:LCD MODULE SPECIFICATION |
| GM123210NFNBB-01 | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:LCD MODULE SPECIFICATION |
發(fā)布緊急采購,3分鐘左右您將得到回復(fù)。