- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄367613 > LUCL8576BP-D Dual Ringing SLIC PDF資料下載
參數(shù)資料
| 型號: | LUCL8576BP-D |
| 英文描述: | Dual Ringing SLIC |
| 中文描述: | 雙振鈴用戶接口 |
| 文件頁數(shù): | 21/26頁 |
| 文件大小: | 583K |
| 代理商: | LUCL8576BP-D |
第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁第11頁第12頁第13頁第14頁第15頁第16頁第17頁第18頁第19頁第20頁當(dāng)前第21頁第22頁第23頁第24頁第25頁第26頁
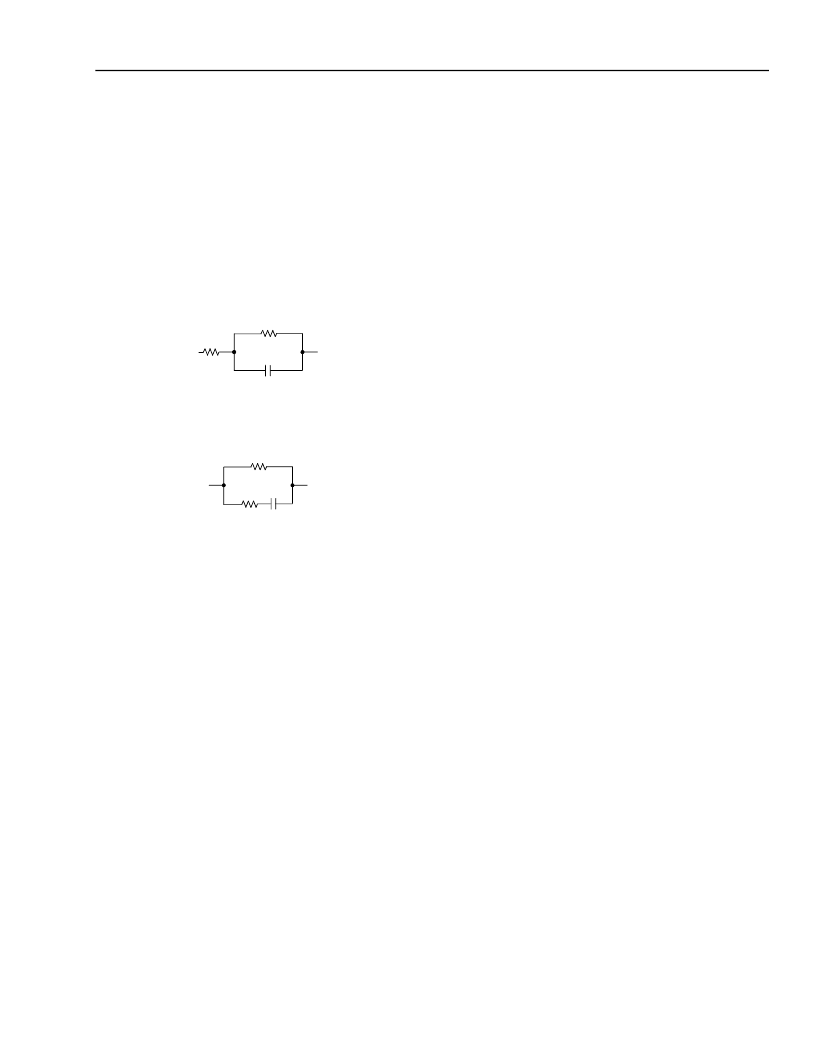
Agere Systems Inc.
21
Data Sheet
May 2001
L8576B Dual Ringing SLIC
Applications
(continued)
ac Design
(continued)
Example 2, Complex Termination
The gain shaping required of a complex termination
impedance can be synthesized using the internal AX
amplifier. The following discussion and equations
present a method for selecting proper component val-
ues for the SLIC/codec interface when using a complex
termination.
Complex termination is usually of the form:
5-6396(F)
To work with this application, convert termination to the
form:
5-6397(F)
where:
R
1
′ = R
1
+ R
2
R
2
′ =
(R
1
+ R
2
)
C′ =
C
For the following discussion, refer to Figure 21.
R
TGP
/R
TGS
/C
TGS
(Z
TG
): These components give gain
shaping to get good gain flatness. These components
are a scaled version of the specified complex termina-
tion impedance. Note for pure (600
) resistive termi-
nations, components R
TGS
and C
TGS
are not used.
Resistor R
TGP
is used and is the series resistance com-
bination of R
GX1
and R
GX2
or 24.4 k
.
R
X
/R
T2
: With other components set, the transmit gain
(for complex and resistive terminations) R
X
and R
T2
are
varied to give specified transmit gain.
R
T1
/R
RCV
/R
GP
: For both complex and resistive termina-
tions, the ratio of these resistors set the receive gain.
For resistive terminations, the ratio of these resistors
set the return loss characteristic. For complex termina-
tions, the ratio of these resistors set the low-frequency
return loss characteristic.
C
N
/R
N1
/R
N2
: For complex terminations, these compo-
nents provide high-frequency compensation to the
return loss characteristic. For resistive terminations,
these components are not used. R
CVN
is connected to
ground via a resistor.
R
HB
: Sets hybrid balance for all terminations.
Set Z
TG
— gain shaping:
Z
TG
= R
TGP
|| R
TGS
+ C
TGS
which is a scaled version of
Z
T/R
(the specified termination resistance) in the
R
1
′ || R
2
′ + C′ form.
R
TGP
must be 24.4 k
to set SLIC transconductance to
125 V/A.
R
TGP
= 24.4 k
At dc, C
TGS
and C′ are open.
R
TGP
= M x R1′
where M is the scale factor.
M =
It can be shown:
R
TGS
= M x R2′
and
C
TGS
=
R
2
C
R
1
R
1
′
C′
R
2
′
1
R
2
-------
+
1
2
---------------------
2
R
1
′
-----------------------
′
M
------
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| LUCL8576BP-DT | Dual Ringing SLIC |
| LUCL9214AAJ-D | GT 19C 19#12 PIN RECP |
| LUCL9214AAJ-DT | Circular Connector; MIL SPEC:MIL-C-5015; Body Material:Metal; Series:GT; No. of Contacts:2; Connector Shell Size:24; Connecting Termination:Solder; Circular Shell Style:Square Flange Receptacle; Body Style:Straight |
| LUCL9214GAJ-D | Low-Cost Ringing SLIC |
| LUCL9214GAJ-DT | Low-Cost Ringing SLIC |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| LUCL8576BP-DT | 制造商:AGERE 制造商全稱:AGERE 功能描述:Dual Ringing SLIC |
| LUCL9214AA-DT | 制造商:AGERE 制造商全稱:AGERE 功能描述:Low-Cost Ringing SLIC |
| LUCL9214AAJ-D | 制造商:AGERE 制造商全稱:AGERE 功能描述:Low-Cost Ringing SLIC |
| LUCL9214AAJ-DT | 制造商:AGERE 制造商全稱:AGERE 功能描述:Low-Cost Ringing SLIC |
| LUCL9214AAU-D | 制造商:AGERE 制造商全稱:AGERE 功能描述:Low-Cost Ringing SLIC |
發(fā)布緊急采購,3分鐘左右您將得到回復(fù)。