參數(shù)資料
型號(hào)： MC145181
廠商： Motorola, Inc.
英文描述： Dual 550/60MHz PLL Frequency Synthesizers with DACs and Voltage Multipliers(帶DACs和電壓乘法器的雙550/60MHzPLL頻率合成器)
中文描述： 雙550/60MHz鎖相環(huán)頻率合成器的DAC和電壓倍增器（帶數(shù)模轉(zhuǎn)換器和電壓乘法器的雙550/60MHzPLL頻率合成器）
文件頁(yè)數(shù)： 66/71頁(yè)
文件大?。?/td> 907K
代理商： MC145181
MC145181
66
MOTOROLA RF/IF DEVICE DATA
by the user. (When the Mode pin is high, programming N23 to
a 0 is for Motorola use only.)
In summary, $895F90 is serially transferred (BitGrabber
access). The N register access also causes double–buffer
transfers of Hr to R and Hn to N .
Step 6: Load the C Register
Now that legitimate divide ratios are programmed for the
counters, the main loop may be activated. Thus, the PD float
bit C4 is now programmed to 0. The standby bits are
unchanged: C2 = C1 = C0 = 0. Bit C5 could be used to control
Output C to either a low level or high impedance; for a low
level, C5 = 0. Whenever an external reference is utilized, bit
C6 must be 1. Bit C7 may be used to control Output A to a low
or high level because it is selected as “port expander” by bit
R 21 and R 20; for a low level, C7 = 0.
In summary, $40 is serially transferred (BitGrabber
access). This causes the main loop to tune to 450 MHz, the
secondary loop to tune to 50 MHz, and both the Output A and
Output C pins to be forced low.
The device is now initialized.
8C. PROGRAMMING WITHOUT ADAPT
Tuning the Top of the Band
After initializing the device via steps 1 through 6 in Section
8B, the only register that needs to be loaded to tune the main
loop is the N register.
For this example, tuning the upper end of the band
(500 MHz) requires that the 5 kHz at the phase/frequency
detector be multiplied up to 500 MHz. This is a loop
multiplying factor of 100,000. This value is converted to
$186A0 and is loaded for bits N17 to N0. Bits N23 to N18 are
not changed and are programmed as indicated in Section 8B,
step 5.
In summary, $8986A0 is transferred to tune the main loop.
No other registers are loaded.
Tuning Other Channels
Tuning other channels for the main loop, while keeping the
secondary loop at a constant frequency, only requires
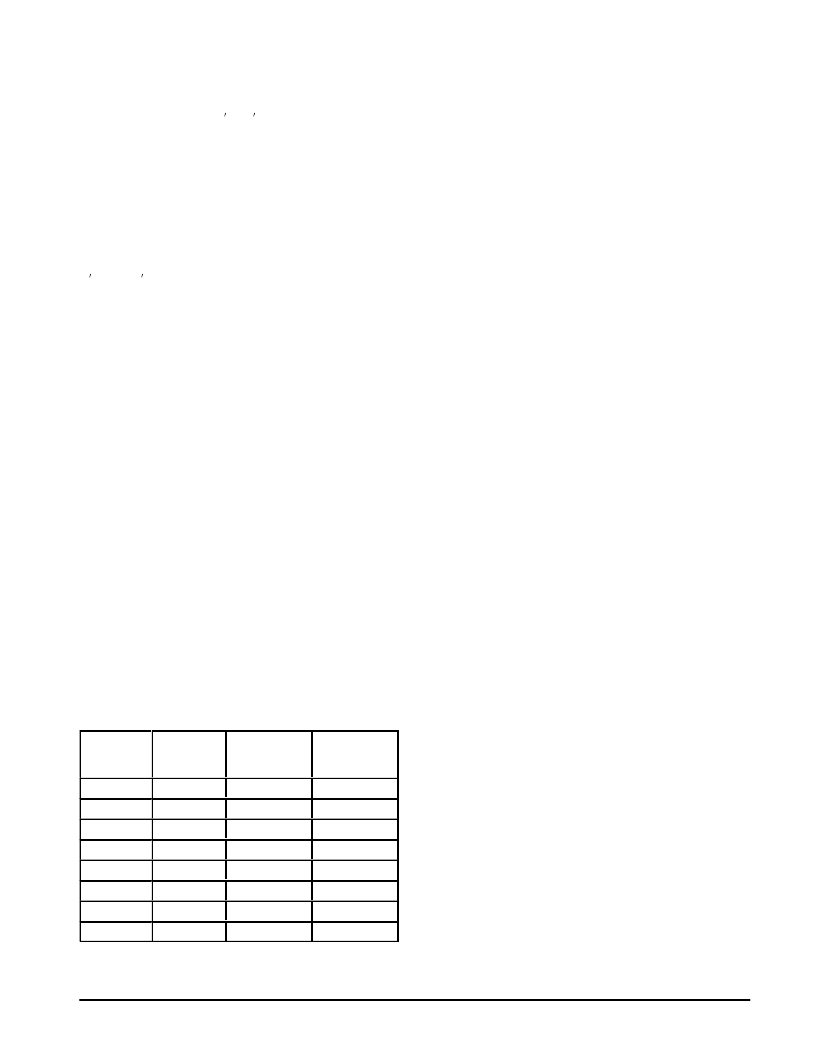
programming the N register. See Table 22 for example
frequencies.
ááááááááááááááá
á
ááááááááááááááá
á
ááá
ááá
ááá
á
(MHz)
á
(Decimal)
á
ááá
ááá
Multiplying
90,000
$15F90
áááá
áááá
100,000
á
á
(Hexadecimal)
á
ááá
ááá
á
á
á
N Register
Data
450.000
90,001
$895F90
ááááááááááááááá
450.005
$15F91
$895F91
ááááááááááááááá
450.010
90,002
$15F92
$895F92
ááááááááááááááá
450.015
90,003
$15F93
$895F93
ááááááááááááááá
455.000
91,000
$16378
$896378
ááááááááááááááá
458.015
91,603
$165D3
$8965D3
ááááááááááááááá
471.040
94,208
$17000
$897000
ááááááááááááááá
500.000
áááá
$186A0
$8986A0
8D. PROGRAMMING UTILIZING HORSESHOE WITH
ADAPT
Introduction
A unique adapt feature can be used with the MC145181
when conventional tuning can not meet the lock–time
requirements of a system and the annoying spurs or noise
can not be tolerated from a fractional–N scheme. The adapt
feature is available on the main loop only.
For adapt, a timer is engaged which causes an internal
data update of the R and N registers to be delayed. The IC
supports the Horseshoescheme for adapt by allowing a
fairly–close quickly–tuned approximatefrequency to be
tuned, followed by the tuning of the exactfrequency. Two sets
of R and N data are sent to the device. The first set {R1, N1}
is for tuning the approximate frequency. The second set {R2,
N2} is for tuning the exact frequency. Use of the timer delays
the transfer of {R2, N2} until a programmed interval has
elapsed. In addition, after the interval has elapsed, the main
loop control switches from PDout–Hi to PDout–Lo.
Tuning Near the Top of the Band
Continuing the example, after initializing the device via
steps 1 through 6 in Section 8B, Horseshoe with adapt can
be used to tune the main loop to obtain fast frequency jumps.
Use of the BitGrabber access is recommended to minimize
the number of serial data clocks required for sending the four
“words”.
In this example, the first phase of adapt utilizes
approximate tuning with the phase/frequency detector
running at 4x the step size. Therefore, the approximate
tuning runs the detector at about 20 kHz. The second phase,
with exact tuning, runs the detector at 5 kHz. Horseshoe with
adapt requires that two data sets be serially sent to the
device for every frequency tuned. The first set is for
approximate tuning {R1, N1}; the second set is for exact
tuning {R2, N2}.
Approximate tuning with Horseshoe is unique. This
method involves two key elements: (1) increasing the phase
detector frequency and (2) varying boththe R and N divide
values such that the approximate frequency is within a
certain predetermined range. The Horseshoe algorithm
contained in the development system software also allows
placing a constraint on the loop–gain variation that the user
can tolerate.
For example, to tune 459.97 MHz, the first {R1, N1} data
set could contain divide ratios for the R and N counters of
973.5 and 23,034, respectively. With this data set, the phase
detector is running at about 19.97 kHz and the approximate
frequency is about 170 Hz from the exact frequency. The
second data set contains R and N divide values of 3,888 and
91,994, respectively. This achieves the exact (target)
frequency of 459.97 MHz.
The timer must be programmed to determine the interval
that the device is in the approximate–tune mode. For this
example, assume this is 32 fR cycles; thus, bits N21 N20
N19 = 1 0 1 in the first data set. Note that this time interval is
32 cycles of fR, with the phase detector running at about
20 kHz (approximate tune) or about 1.6 ms plus the MCU
shift time shown in Figure 64. Included in the first data set are
N23 = 1 which is required when the Mode pin is high, N22 = 0
相關(guān)PDF資料
PDF描述
MC145193 1.1GHz PLL Frequency Synthesizer(1.1GHz PLL頻率合成器)
MC145202-1 PLL Frequency Synthesizer(2.0GHz PLL頻率合成器)
MC145225 Dual PLL Frequency Synthesizers With DACs and Voltage Multipliers(帶DACs和電壓乘法器的雙PLL頻率合成器)
MC145230 Dual PLL Frequency Synthesizers With DACs and Voltage Multipliers(帶DACs和電壓乘法器的雙PLL頻率合成器)
MC14528BCL Dual Monostable Multivibrator
相關(guān)代理商/技術(shù)參數(shù)
參數(shù)描述
MC14518BCP 功能描述:計(jì)數(shù)器移位寄存器 3-18V Dual BCD Up RoHS:否 制造商:Texas Instruments 計(jì)數(shù)器類型: 計(jì)數(shù)順序:Serial to Serial/Parallel 電路數(shù)量:1 封裝 / 箱體:SOIC-20 Wide 邏輯系列: 邏輯類型: 輸入線路數(shù)量:1 輸出類型:Open Drain 傳播延遲時(shí)間:650 ns 最大工作溫度:+ 125 C 最小工作溫度:- 40 C 封裝:Reel
MC14518BCPG 功能描述:計(jì)數(shù)器移位寄存器 3-18V Dual BCD Up RoHS:否 制造商:Texas Instruments 計(jì)數(shù)器類型: 計(jì)數(shù)順序:Serial to Serial/Parallel 電路數(shù)量:1 封裝 / 箱體:SOIC-20 Wide 邏輯系列: 邏輯類型: 輸入線路數(shù)量:1 輸出類型:Open Drain 傳播延遲時(shí)間:650 ns 最大工作溫度:+ 125 C 最小工作溫度:- 40 C 封裝:Reel
MC14518BDW 功能描述:計(jì)數(shù)器移位寄存器 3-18V Dual BCD Up RoHS:否 制造商:Texas Instruments 計(jì)數(shù)器類型: 計(jì)數(shù)順序:Serial to Serial/Parallel 電路數(shù)量:1 封裝 / 箱體:SOIC-20 Wide 邏輯系列: 邏輯類型: 輸入線路數(shù)量:1 輸出類型:Open Drain 傳播延遲時(shí)間:650 ns 最大工作溫度:+ 125 C 最小工作溫度:- 40 C 封裝:Reel
MC14518BDWG 功能描述:計(jì)數(shù)器移位寄存器 3-18V Dual BCD Up RoHS:否 制造商:Texas Instruments 計(jì)數(shù)器類型: 計(jì)數(shù)順序:Serial to Serial/Parallel 電路數(shù)量:1 封裝 / 箱體:SOIC-20 Wide 邏輯系列: 邏輯類型: 輸入線路數(shù)量:1 輸出類型:Open Drain 傳播延遲時(shí)間:650 ns 最大工作溫度:+ 125 C 最小工作溫度:- 40 C 封裝:Reel
MC14518BDWR2 功能描述:計(jì)數(shù)器移位寄存器 3-18V Dual BCD Up RoHS:否 制造商:Texas Instruments 計(jì)數(shù)器類型: 計(jì)數(shù)順序:Serial to Serial/Parallel 電路數(shù)量:1 封裝 / 箱體:SOIC-20 Wide 邏輯系列: 邏輯類型: 輸入線路數(shù)量:1 輸出類型:Open Drain 傳播延遲時(shí)間:650 ns 最大工作溫度:+ 125 C 最小工作溫度:- 40 C 封裝:Reel
發(fā)布緊急采購(gòu)，3分鐘左右您將得到回復(fù)。

采購(gòu)需求

(若只采購(gòu)一條型號(hào)，填寫(xiě)一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

*型號(hào) *數(shù)量 廠商 批號(hào) 封裝
添加更多采購(gòu)

我的聯(lián)系方式

*
*
*