參數(shù)資料
型號(hào)： HSP43216JC-52Z
廠商： Intersil
文件頁(yè)數(shù)： 19/20頁(yè)
文件大小： 0K
描述： IC HALFBAND FILTER 84-PLCC
標(biāo)準(zhǔn)包裝： 15
濾波器類型： 半帶
濾波器數(shù)： 4
電源電壓： 4.75 V ~ 5.25 V
安裝類型： 表面貼裝
封裝/外殼： 84-LCC（J 形引線）
供應(yīng)商設(shè)備封裝： 84-PLCC（29.21x29.21）
包裝： 管件
8
FN3365.10
October 6, 2008
Operational Modes
Decimate By 2 Filter Mode (Mode1-0 = 00)
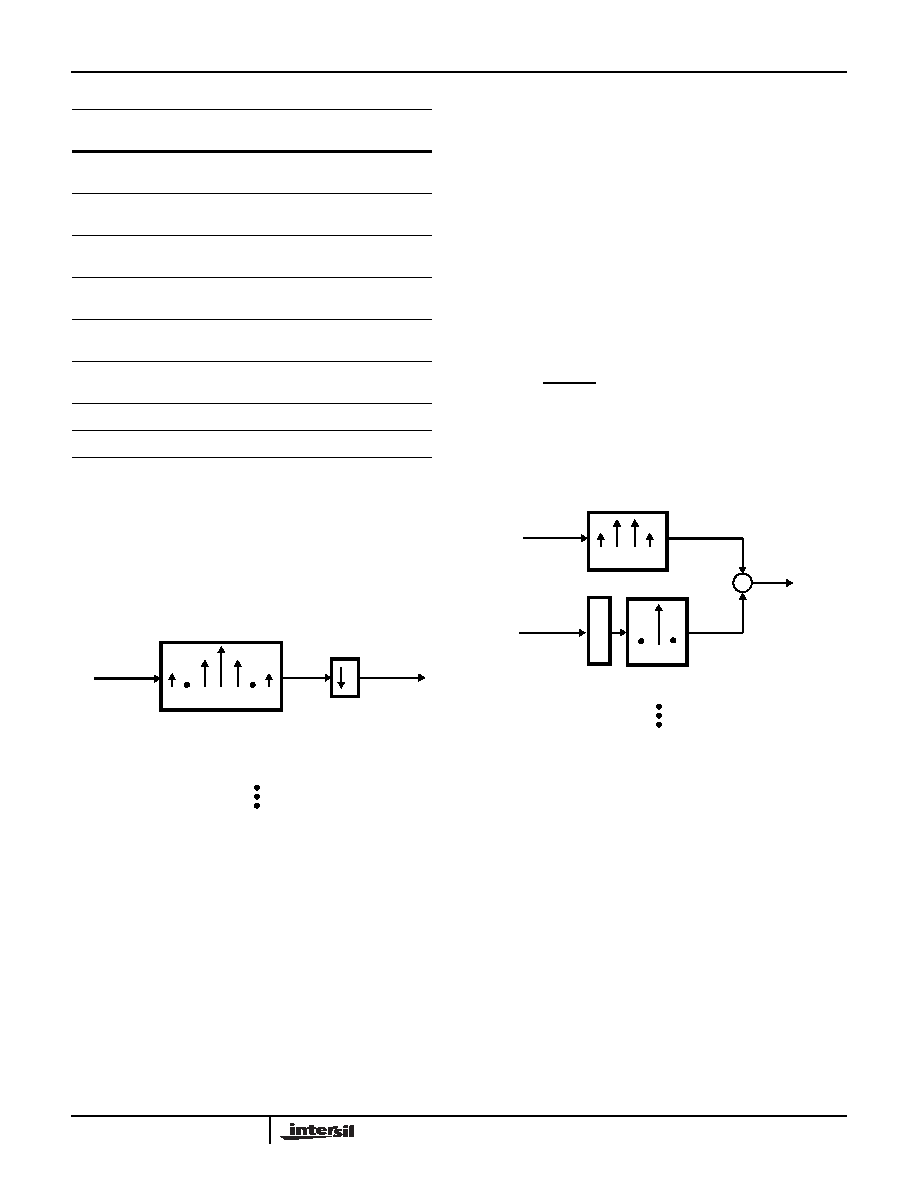
The concept of operation for Decimate by Two Filter mode is
most easily understood by comparing the 7 tap transversal
filter implementation to the equivalent polyphase
implementation. The transversal implementation is shown in
Figure 5.
By inspecting the sum-of-products for the decimated output
in Figure 5, it is seen that even indexed input samples are
always multiplied by the even filter coefficients and the odd
samples are always multiplied by the odd coefficients. This
computational partitioning is realized in the polyphase
implementation shown in Figure 6.
In the polyphase implementation, the input data is broken into
even and odd sample streams which are processed by a set
of polyphase filters running at one half of the input data rate.
These filters are designated as even or odd tap filters
depending upon whether the coefficients were derived from
the even or odd indexed coefficients of the original transversal
filter. This architecture only produces the outputs which are
not discarded by the decimation process. NOTE: Since the
only non-zero tap for a halfband filter is the center tap,
the Odd Tap Filter reduces to a delay and multiply
operation.
The operation of the HSP43216 in Decimate by Two mode is
analogous to the polyphase implementation in Figure 6. In
this mode, the internal data paths are routed as shown in
Figure 7A and Figure 7B. The different data flows depend on
whether internal or external multiplexing has been selected
using the INT/EXT control input. In either case, an input data
stream is decomposed into even and odd sample streams
which are then routed to the even and odd tap polyphase
filters. The output of each polyphase filter is summed and
output via AOUT0-15.
TABLE 5. OUTPUT ROUNDING CONTROL
RND
2-0
ROUND FUNCTION
000
Round output to 8-bits, AOUT15-8 and BOUT15-8, zero
lower bits.
001
Round output to 9-bits, AOUT15-7 and BOUT15-7, zero
lower bits.
010
Round output to 10-bits, AOUT15-6 and BOUT15-6,
zero lower bits.
011
Round output to 11-bits, AOUT15-5 and BOUT15-5,
zero lower bits.
100
Round output to 12-bits, AOUT15-4 and BOUT15-4,
zero lower bits.
101
Round output to 14-bits, AOUT15-2 and BOUT15-2,
zero lower bits.
110
Round output to 16-bits, AOUT15-0 and BOUT15-0.
111
Zero all outputs.
C0 C1 C2 C3 C4 C5 C6
X3,X2,X1,X0
Y(0) = X0(C0)+X1(C1)+X2(C2)+X3(C3)+X4(C4)+X5(C5)+X6(C6)
Y(1) = X1(C0)+X2(C1)+X3(C2)+X4(C3)+X5(C4)+X6(C5)+X7(C6)
Y(2) = X2(C0)+X3(C1)+X4(C2)+X5(C3)+X6(C4)+X7(C5)+X8(C6)
Y(3) = X3(C0)+X4(C1)+X5(C2)+X6(C3)+X7(C4)+X8(C5)+X9(C6)
...,Y1,Y0
2
..,Y4,Y2,Y0
Indicates samples discarded by decimation process
FIGURE 5. TRANSVERSAL IMPLEMENTATION OF
DECIMATE BY 2 HALFBAND FILTER
C0 C2 C4 C6
...,X4,X2,X0
Y(0) = X0(C0)+X1(C1)+X2(C2)+X3(C3)+X4(C4)+X5(C5)+X6(C6)
Y(1) = X2(C0)+X3(C1)+X4(C2)+X5(C3)+X6(C4)+X7(C5)+X8(C6)
..,Y2,Y1,Y0
C1 C3 C5
R
E
G
ODD TAP FILTER
EVEN TAP FILTER
...,X5,X3,X1
+
FIGURE 6. POLYPHASE IMPLEMENTATION OF DECIMATE
BY 2 HALFBAND FILTER
HSP43216
相關(guān)PDF資料
PDF描述
HSP43220JC-33Z IC DECIMATING DGTL FILTER 84PLCC
IA188EM-PTQ100I-R-03 IC MCU 8/16BIT 40MHZ 100TQFP
IA188ES-PTQ100I-R-03 IC MCU 8/16BIT 40MHZ 100TQFP
IA6805E2PLC44IR0 IC MCU 8BIT 5MHZ 44PLCC
IA82050-PDW28I-R-01 IC ASYNCHRONOUS SERIAL CTRL
相關(guān)代理商/技術(shù)參數(shù)
參數(shù)描述
HSP43216JI-52 制造商:Rochester Electronics LLC 功能描述:- Bulk
HSP43216VC-52 功能描述:有源濾波器 HALFBAND FILTER 100 PIN PQFP,COMM RoHS:否 制造商:Maxim Integrated 通道數(shù)量:1 截止頻率:150 KHz 電源電壓-最大:11 V 電源電壓-最小:4.74 V 最大工作溫度:+ 85 C 安裝風(fēng)格:Through Hole 封裝 / 箱體:PDIP N 封裝:Tube
HSP43216VC-52Z 功能描述:有源濾波器 W/ANNEAL HALFB & FILER 100 PIN PQFP RoHS:否 制造商:Maxim Integrated 通道數(shù)量:1 截止頻率:150 KHz 電源電壓-最大:11 V 電源電壓-最小:4.74 V 最大工作溫度:+ 85 C 安裝風(fēng)格:Through Hole 封裝 / 箱體:PDIP N 封裝:Tube
HSP43220 制造商:INTERSIL 制造商全稱:Intersil Corporation 功能描述:Decimating Digital Filter
HSP43220/883 制造商:INTERSIL 制造商全稱:Intersil Corporation 功能描述:Decimating Digital Filter
發(fā)布緊急采購(gòu)，3分鐘左右您將得到回復(fù)。

采購(gòu)需求

(若只采購(gòu)一條型號(hào)，填寫(xiě)一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

*型號(hào) *數(shù)量 廠商 批號(hào) 封裝
添加更多采購(gòu)

我的聯(lián)系方式

*
*
*