參數(shù)資料
型號： MC145225
廠商： Motorola, Inc.
英文描述： Dual PLL Frequency Synthesizers With DACs and Voltage Multipliers(帶DACs和電壓乘法器的雙PLL頻率合成器)
中文描述： 雙鎖相環(huán)頻率合成器與DAC和電壓倍增器（帶數(shù)模轉(zhuǎn)換器和電壓乘法器的雙鎖相環(huán)頻率合成器）
文件頁數(shù)： 32/71頁
文件大小： 906K
代理商： MC145225
MC145225 MC145230
32
MOTOROLA RF/IF DEVICE DATA
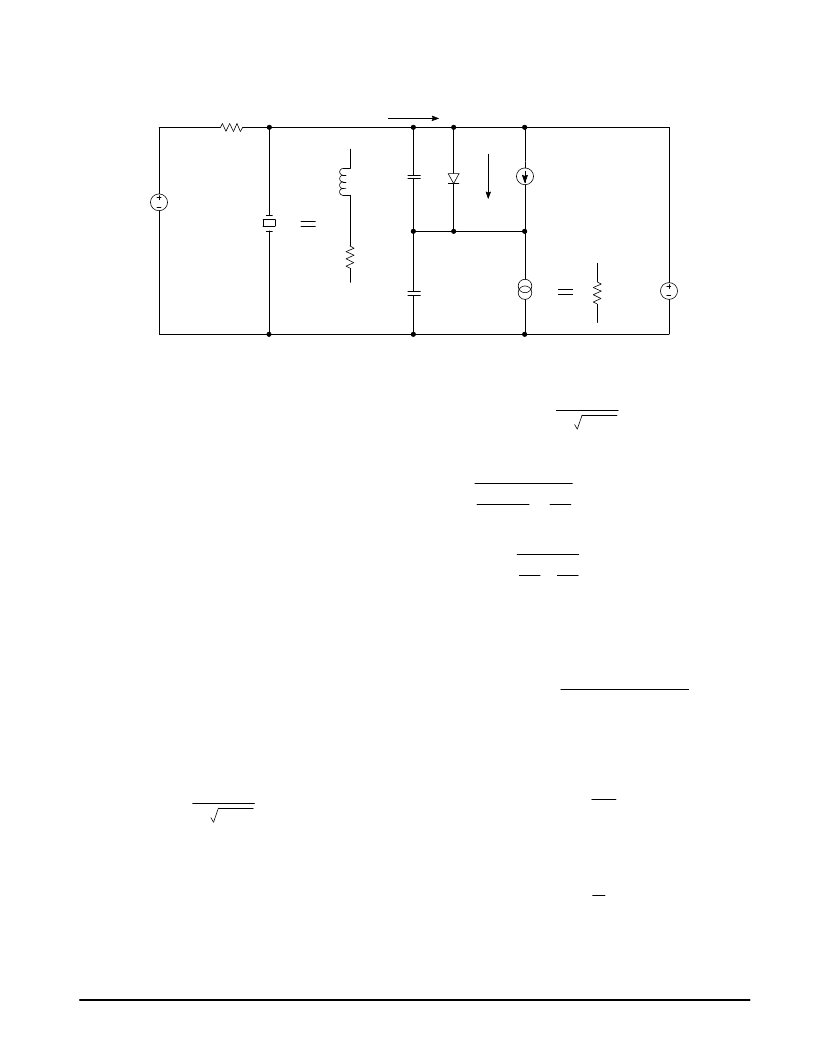
Figure 27. Equivalent Circuit for Crystal Power Estimation
C2
C1
Rs
Re
200/800
μ
A
X1
I1
Blb
lb
Ls
VCC x R2 / (R1 + R2)
R1 || R2
Iin
VCC
Overtone Operation
For overtone operation, the circuit is modified by the
addition of an inductor, L1; and a series capacitor, C4. C4 is
inserted as a dc blocking capacitor whose capacitance is
chosen sufficiently large so that its reactance can be ignored.
This circuit is shown in Figure 28.
For oscillation to occur at the overtone frequency, the
condition
gm Zc1 Zc2 > Rs
must exist.
Zc1 represents the impedance across C1 and can be
defined as
Zc1 = jXc1||(Rl1 + jXl1)
where Rl1 is the dc resistance of the inductor L1.
For overtone operation, this must occur at the desired
harmonic. For example, if the crystal is chosen to oscillate at
the third overtone, C1 and C2 must be chosen so that the
above condition exists for Zc1 and Zc2 at the third harmonic of
the fundamental frequency for the crystal. In addition, care
must be taken that the “negative resistance” of the amplifier is
not sufficient at the fundamental frequency to induce
oscillation at the fundamental frequency. It may be necessary
to add additional filtering to reduce the gain of the amplifier at
the fundamental frequency. The key to achieving stable
overtone oscillator operation is ensuring the existence of the
above condition at the desired overtone while ensuring its
failure at all other frequencies.
L1 and C1 are chosen so that
1
> Ff
2
π
L1 C1
where Ff is the fundamental frequency of the crystal
resonator. If L1 and C1 are chosen to be net capacitive at the
desired overtone frequency and if the condition
gm Zc1 Zc2 > Rs
is true only at the desired overtone frequency, the oscillator
will oscillate at the frequency of the overtone. Normally, L1
and C1 are not chosen to be resonant at the overtone
frequency but at a lower frequency to ensure that the parallel
combination of L1 and C1 is capacitive at the overtone
frequency and inductive at the fundamental frequency.
1
Ff <
< Fo
2
π
L1 C1
The net inductance of the rest of the resonant loop then
balances this capacitance at the overtone frequency.
1
1
Xls – Xcs
Xc0
–
+ Xl2 + Xl(stray) – Xc3
1
1
–
= 0
1
Xc1
1
Xl1
+
L2 and C3 are chosen to provide the desired adjustment to
the resonant overtone frequency. This is normally computed
by calculating the expected ppm change at the resonant
frequency and using this to define the value of the reactance
necessary to produce this change.
X (of L2 and C3)
Z (crystal at resonance)
Ff (ppm) =
Ff (ppm) = X(of L2 and C3)/Z(crystal at resonance)
The values needed for this calculation can be derived from
the value of the fundamental frequency and Co. If Co is
known or can be measured, Cs is defined as
200
Co
Cs =
for an AT cut crystal.
The fundamental frequency can be used to calculate the
value for Ls using either the series resonant or parallel
resonant formulas given earlier. Since the Q of the crystal,
R
X
Q =
is usually sufficiently large at the resonant frequency so that
Rs << Z(crystal)
相關(guān)PDF資料
PDF描述
MC145230 Dual PLL Frequency Synthesizers With DACs and Voltage Multipliers(帶DACs和電壓乘法器的雙PLL頻率合成器)
MC14528BCL Dual Monostable Multivibrator
MC14528 DEFLECTION PROCESSOR FOR MULTISYNC MONITORS
MC14528 Dual Monostable Multivibrator
MC14528BFEL Dual Monostable Multivibrator
相關(guān)代理商/技術(shù)參數(shù)
參數(shù)描述
MC14522BCP 制造商:Motorola Inc 功能描述:Counter, Down, Decade, 16 Pin, Plastic, DIP
MC14522BDW 制造商:Motorola Inc 功能描述:
MC14526B AC7 WAF 制造商:ON Semiconductor 功能描述:
MC14526BAC7 WAF 制造商:ON Semiconductor 功能描述:
MC14526BCL 制造商: 功能描述: 制造商:undefined 功能描述:
發(fā)布緊急采購，3分鐘左右您將得到回復(fù)。

采購需求

(若只采購一條型號，填寫一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購。也可以進入我的后臺，查看報價

發(fā)布成功！您可以繼續(xù)發(fā)布采購。也可以進入我的后臺，查看報價

*型號 *數(shù)量 廠商 批號 封裝
添加更多采購

我的聯(lián)系方式

*
*
*